MIPS: control

En el último artículo vimos como funcionaban la ALU y los registros en la CPU de MIPS formando un datapath, al menos para un subconjunto de las instrucciones de la arquitectura.

Ahora agregamos la pieza que falta, la unidad de control. Pueden ver la implementación de la misma en Logisim en la rama control de este repo.

Contenidos

1. Señales de control
2. ALU Control
3. Implementando el control
4. Una tabla de 256 filas
5. Conclusión

Señales de control

Lo primero que hay que hacer es identificar las señales de control para el datapath que describimos en el artículo anterior. Son en general líneas de 1 bit de ancho que le indican a las unidades funcionales como el archivo de registros o la ALU que operación realizar. Las resumo en la siguiente tabla.

Nombre	Ancho	Efecto
RegDst	1 bit	Según tengamos una instrucción de tipo R o tipo I el registro de destino puede venir de rt o rd. Esta señal controla el mux que elige entre estas dos opciones.
RegWrite	1 bit	Para que el archivo de registros escriba en el registro de destino esta señal tiene que estar activada.
ALUSrc	1 bit	Esta señal controla el segundo input de la ALU a través de un mux. O viene del archivo de registros o del campo imm de la instrucción.
MemRead	1 bit	Para leer de la memoria de datos esta señal tiene que valer 1.
MemWrite	1 bit	Para escribir en la memoria de datos esta señal tiene que valer 1.
MemToReg	1 bit	El valor para la etapa de write back proviene de la memoria de datos si vale 1 o de la ALU si vale 0.
Jump	1 bit	Esta señal vale 1 cuando la instrucción es un jump.
Branch	1 bit	Esta señal vale 1 cuando la instrucción es un branch.
ALU Op	2 bits	Esta señal de dos bits es una de las entradas de la unidad de control de la ALU. Se detalla su funcionamiento en una tabla aparte.

Todas las señales de control definidas en la tabla de arriba se determinan en base a los 6 bits del opcode, presente en los bits 26 a 31 de la instrucción. La unidad de control recibe estos 6 bits como entrada y produce como salida la combinación de unos y ceros correcta en las salidas que detallamos en la tabla.

La única unidad funcional del datapath que falta controlar es la ALU, que recibe 4 bits como señal de control indicando que operación realizar. Estos 4 bits provienen de una unidad de control de la ALU llamada ALU Control en el diagrama del datapath.

ALU Control

Las operaciones posibles de la ALU para el subconjunto de instrucciones considerado se resumen en la siguiente tabla.

ALU Control	Operación
0010	suma
0110	resta
0000	AND
0001	OR

Para el caso de las instrucciones de tipo R la combinación de los dos bits de ALU Op que vienen de la unidad de control más los 6 bits del campo funct de la instrucción determinan los 4 bits de control de la ALU.

En cambio para instrucciones de tipo I que también utilizan la ALU el campo funct no está presente, así que ALU Control setea los 4 bits de su salida en base a los dos bits de ALU Op únicamente. La siguiente tabla resume este funcionamiento. Las “x” significan que no nos importa el valor de ese campo o entrada.

Instrucción	ALU Op	funct	Operación de la ALU	ALU Control
lw	00	xxxxxx	suma	0010
sw	00	xxxxxx	suma	0010
beq	01	xxxxxx	resta	0110
add	10	100000	suma	0010
sub	10	100010	resta	0110
and	10	100100	AND	0000
or	10	100101	OR	0001

Noten que las instrucciones de tipo R (opcode 0x00) siempre setean las líneas de ALU Op con el valor $10_2$.

Implementando el control

La implementación de las dos unidades de control mencionadas es un ejercicio de lógica combinacional. La unidad de control que decodifica el opcode puede pensarse como una función booleana de 6 entradas y 10 salidas. En principio uno puede construir una tabla de verdad de $2^6 = 64$ filas y diez columnas de salida y minimizar cada una de ellas.

Pero hay una manera más simple de pensar el problema, usando una tabla resumida para considerar solo los casos que esperamos que sucedan en el circuito completo de la CPU.

instrucción	opcode	control word
lw	100011	0111100000
sw	101011	0100010000
j	000010	0000000100
beq	000100	0000001001
Tipo R	000000	1001000010

Para no tener demasiadas columnas en la tabla armo lo que se conoce como control word que no es más que la concatenación de los diez bits de las señales de control como si fueran un único dato. El orden utilizado para las señales de control de izquierda a derecha es el siguiente: RegDst, ALUSrc, MemToReg, RegWrite, MemRead, MemWrite, Branch, Jump, ALU Op 1 y ALU Op 0.

Con esto podemos armar un circuito con un plano de compuertas AND y otro de compuertas OR. Las compuertas AND decodifican los opcodes, obteniendo un uno solamente en la compuerta correspondiente al opcode en la entrada de la unidad de control. Ese valor se traslada a las salidas indicadas en la tabla de arriba.

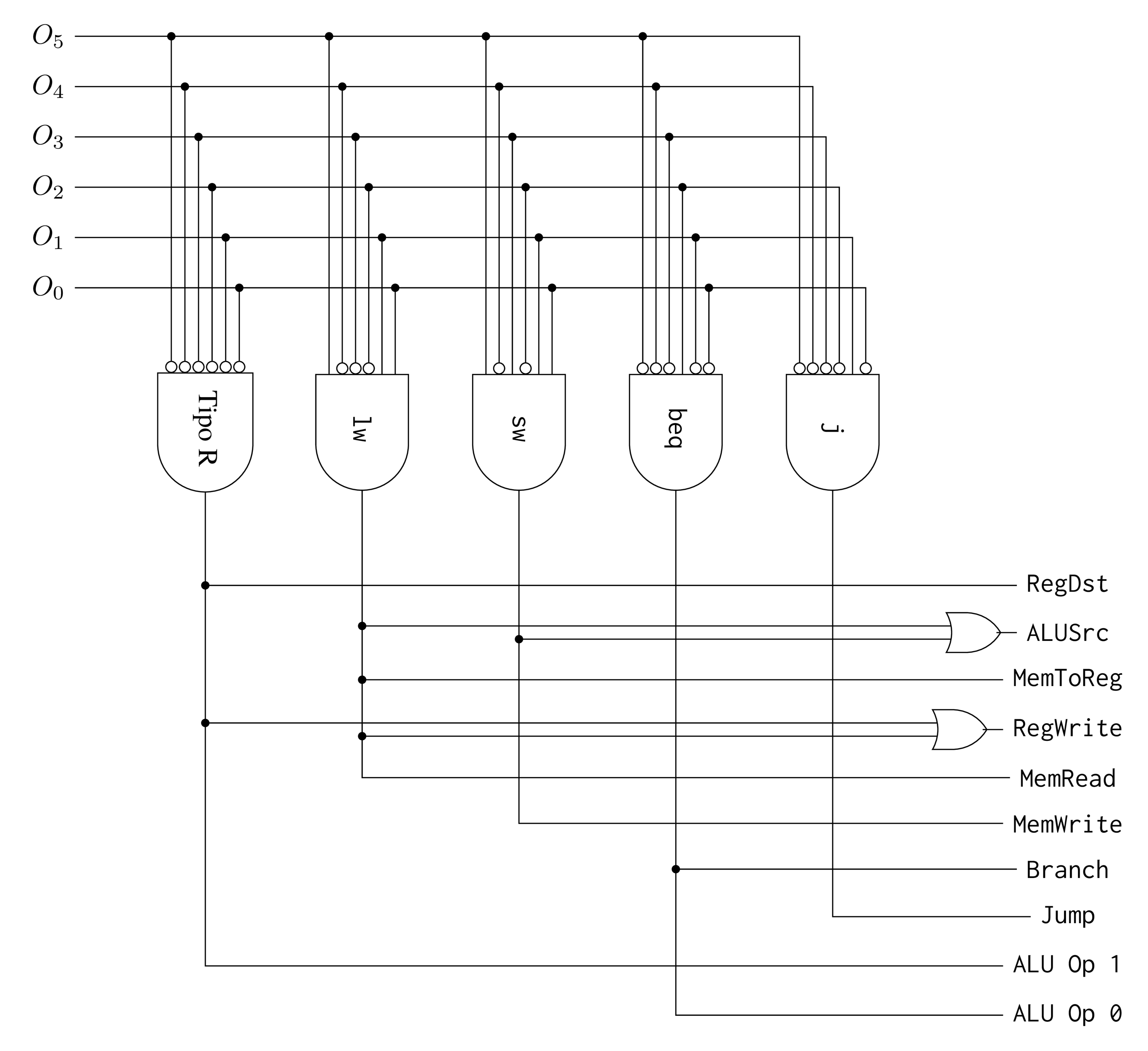
Una tabla de 256 filas

Para implementar la lógica de ALU Control recordemos que necesitamos producir una señal de 4 bits a partir de los 2 bits de ALU Op y los 6 bits del campo funct. Tenemos una función booleana de 8 entradas y 4 salidas. Si intentamos armar una tabla para ver todos los casos posibles tenemos $2^8=256$ combinaciones posibles (filas de la tabla).

Por suerte no estamos implementando la totalidad de las instrucciones de MIPS, solo tenemos que ocuparnos de sw, lw, beq, j, and, or, add y sub. Si ponemos la información que tenemos en una tabla vemos que podemos ignorar algunas de las entradas.

Instrucción	ALU Op	funct	ALU Control
lw	00	xxxxxx	0010
sw	00	xxxxxx	0010
beq	01	xxxxxx	0110
add	10	100000	0010
sub	10	100010	0110
and	10	100100	0000
or	10	100101	0001

Los bits 3, 4 y 5 del campo funct son iguales para las cuatro instrucciones de tipo R que estamos considerando así que los ignoramos a la hora de hacer el circuito. El último bit de ALU Control es cero en todos los casos así que tampoco lo tenemos en cuenta. Claro que en la CPU completa con todas las instrucciones esta simplificación no sería válida.

La función ahora se reduce a 5 entradas y 3 salidas. Podemos construir la tabla de 32 filas, buscar la FND y minimizar. O podemos intentar derivar de la tabla de arriba una ecuación para cada uno de los 4 bits de la salida.

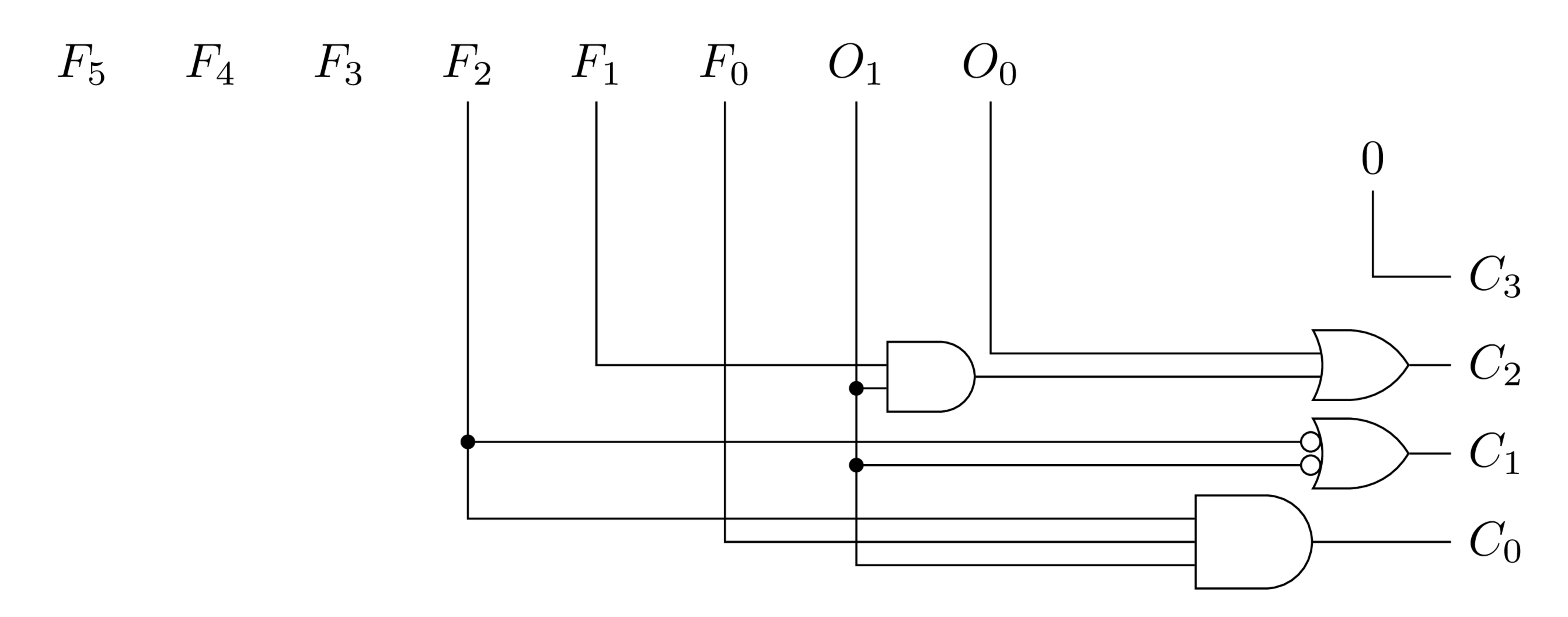
Voy a nombrar a cada bit de la salida ALU Control con la letra $C$ y un subíndice. El más fácil es obviamente $C_3 = 0$ como se ve en la tabla.

$C_2$ vale uno solo cuando queremos hacer una resta. O bien porque estamos en un beq y ALU Op vale 01 o porque estamos en un sub y ALU Op vale 10 y $F_1$ vale 1. Acá la letra $F$ representa al campo funct, los bits numerados desde el 0 al 5 contando desde el bit menos significativo. La ecuación queda $C_2 = O_0 + O_1F_1$. Donde $O_1$ y $O_0$ son los bits de ALU Op.

$C_1$ vale 1 salvo para and y or. Podemos resolver con una compuerta OR con sus entradas negadas. En primer lugar $O_1$ no tiene que ser 1, que solo pasa en las instrucciones tipo R. En segundo lugar si $O_1$ valiera 1, $F_2$ no puede ser 1 porque estaríamos en un and o en un or. La ecuación sería $C_1=\bar{O_1}+\bar{F_2}$.

Por último $C_0$ solo vale 1 para el or. La ecuación es directa, un AND entre las tres entradas que deben ser 1 para que la instrucción sea or. $C_0=O_1F_2F_0$. El circuito completo quedaría como se ilustra abajo.

Conclusión

Lo que acabamos de hacer es lo que se conoce como una implementación hardwired del control en una CPU. Al considerar un pequeño conjunto de las instrucciones de MIPS la tarea es relativamente sencilla.

En definitiva la lógica combinacional que implementa una unidad de control es en gran parte un decodificador. Traduce opcodes o alguna entrada similar a las señales de control apropiadas.

No dejen de ver el circuito completo de la CPU de este artículo y el anterior en GitHub. La rama master tiene solo la implementación del datapath y la rama control lo que se explica en este artículo, completando esta versión simplificada de la CPU de MIPS.

Escrito el 26 de Noviembre de 2020 por Santiago Trini